¿Y si en lugar de aplicar la Ley D'Hondt hacemos como en los consejos?
El método que utilizan las empresas sería más fiel al resultado electoral, pero dificultaría la gobernabilidad

La consolidación de nuevos partidos políticos y el agotamiento del bipartidismo han generado un creciente cuestionamiento de la ley electoral. Se argumenta que es necesario revisarla para que el arco político sea más justo a la hora de asignar los escaños y no favorezca el mantenimiento de aquellos dos partidos, o bloques de partidos, que tradicionalmente gobiernan los países europeos desde la segunda guerra mundial.
En la búsqueda de alterativas a la forma de repartir los escaños en los parlamentos, ¿serviría ver cómo es el funcionamiento en las grandes empresas -las sociedades anónimas-, a la hora de elegir sus consejos de administración? Merece la pena comprobar si pudiera ser una alternativa válida y facilitar la reforma electoral.
Hay acuerdo general en la necesidad de facilitar la representación de las minorías en las elecciones, pero, a la vista de lo sucedido en Italia, en Cataluña y lo que anuncian las encuestas para las elecciones generales españolas, también parece necesario garantizar que la mayoría pueda tomar decisiones y gobernar. ¿Debe primar la correcta y justa representación o se debe favorecer la gobernabilidad a toda costa? La ley no exige un número mínimo de votos para que una persona sea designada como consejero de una sociedad anónima y sí exige un número mínimo de votos para obtener un escaño.
En España, el reparto de escaños se hace a través de la regla Jefferson, también denominada D´Hondt, por el nombre del profesor belga que la propuso, mientras que en el ámbito de las sociedades anónimas el consejo de administración se crea a partir de la regla de Hamilton. La ley D´Hont favorece a los partidos mayoritarios y la de Hamilton a los minoritarios, por lo que, dependiendo del sistema aplicado, los repartos de las representaciones son diferentes.
La ley D´Hondt se basa en que el coste medio en votos para conseguir un escaño sea sensiblemente el mismo para cada grupo. Para ello, cada escaño se asigna al grupo político que presenta una media más elevada de votos por escaño. No premia simplemente los votos obtenidos en cada lugar, sino que lo hace en función de los votos posibles totales en la demarcación, lo que se traduce en una necesidad distinta de votos, en cada lugar, para obtener un escaño. En demarcaciones electorales con pocos votantes el número de votos necesario para obtener el escaño es menor que en otras con mayor número de votantes.
La regla de Hamilton asigna la representación según la división del número de votos de cada grupo entre la cuota, es decir, según los números enteros de dichos cocientes. Si, después de haber realizado este cálculo faltaran representantes por asignar, aquellos grupos con restos mayores recibirían un puesto adicional. Por lo tanto, y en un hipotético uso político, los escaños pendientes se asignarían a los grupos políticos que tienen los restos mayores.
Las fórmulas distributivas de media mayor, como la regla D´Hondt, favorecen a los grupos mayoritarios, mientras que las fórmulas distributivas de resto mayor, como la de Hamilton, son favorables a una distribución de escaños más fiel a la distribución de votos entre candidaturas. Sin embargo, estas fórmulas de resto mayor, como la de Hamilton, se aplican con mínimos electorales que impiden el acceso al escaño de grupos que no superen un determinado volumen de votos. Es decir, se establece un mínimo para evitar que la representación en un territorio se pueda obtener con un número mucho menor de votos que en otro.
El método D´Hondt favorece a las mayorías, lo que facilita la gobernabilidad y la toma rápida de decisiones. Además, es sencillo de entender y comúnmente utilizado cuando se necesita una representación lo más proporcional posible.
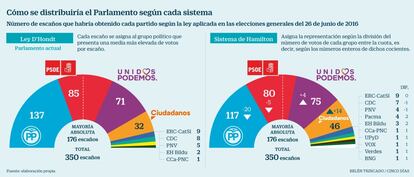
¿Cómo quedaría el reparto de escaños en el parlamento español, con los resultados de las últimas elecciones generales, si aplicáramos el método de reparto de Hamilton, comparado con el actual reparto de la Ley DHónt?
El número de partidos con representación parlamentaria pasaría de 9 a 14, ganando el hemiciclo en diversidad, pero dificultando la obtención de mayorías absolutas individuales y la gobernabilidad por pactos. Entre los 4 grandes partidos, el Partido Popular sería el gran perjudicado, restando 20 escaños a sus actuales 137, quedando en 117; el PSOE perdería 5 parlamentarios, por los 4 que ganaría Unidos Podemos y los 14 que sumaría Ciudadanos. En el resto del hemiciclo, más allá de ligeros bailes de un escaño arriba o abajo en los restantes partidos ya presentes, asistiríamos a un rosario de pequeños partidos con mínima representación, por debajo de la requerida para la obtención de grupo parlamentario y que hoy no participan de la vida parlamentaria, como PACMA, con 4 escaños, y UPyD, los Verdes, BNG y VOX, con un escaño cada uno. En cuanto a pactos de gobernabilidad, la suma de PP y Ciudadanos se quedaría en 163, por los 169 actuales, aún más lejos de la mayoría absoluta; al igual que la del PSOE con Podemos, que pierde 1 escaño frente al reparto D´Hont.
En general, la gobernabilidad sería aún más difícil, y la mayoría absoluta a través de pactos exigiría el acuerdo de 4 o hasta 5 partidos, si atendemos a las actuales preferencias e incompatibilidades entre partidos. Plantearnos, por tanto, una reforma electoral sobre la base de un sistema de reparto de escaños que atienda su asignación en función del número de votos y de restos mayores, puede dar lugar a una mayor participación política de grupos minoritarios, pero corremos el riesgo de enfrentarnos a escenarios de aún más difícil gobernabilidad. Si los partidos políticos se acostumbraran a pactar con mayor facilidad, a semejanza de lo que sucede en Alemania, el cambio sería menos traumático, pero inquieta asistir al caso italiano, con 64 gobiernos y 28 primeros ministros desde la fundación de la república en 1946.
Omar de la Cruz y Fernando Tomé son Profesor de Administración de Empresas/ Decano de la Facultad de Ciencias Sociales. Universidad de Nebrija